The generalized (Extreme Studentized Deviate) ESD test#
Purpose#
The generalized ESD test detects one or more outliers in a dataset that is assumed to be normally distributed.
You must specify the maximum number of outliers, r, to test for.
How it works#
The generalized ESD test essentially performs r separate tests: a test for one outlier, a test for two outliers, and so on until r outliers.
First, a null hypothesis (\(H_{0}\)) is defined. In this case, H₀ assumes that there are no outliers in the dataset. The alternative hypothesis (\(H_{a}\)) is that there are up to r outliers in the dataset.
Next, for each step, we calculate the generalized ESD test statistic, \(R_{i}\)
with \(\overline{x}\) and s denoting the sample mean and standard deviation, respectively.
Remove the observation that maximizes \(|x_{i}-\overline{x}|\) and then recompute the above statistic with n - 1 observations.
Repeat this process until r observations have been removed. This results in the r test statistics \(R_{1}\), \(R_{2}\), …, \(R_{r}\).
At the same time, compute the following corresponding critical values
where \(t_{p,\nu}\) is the critical value from the t distribution with \(\nu\) degrees of freedom and
The number of outliers is determined by finding the largest i such that \(R_{i}\) > \(\lambda_{i}\).
Example#
# Import the libraries needed
import matplotlib.pyplot as plt # For creating visualizations and plots
import numpy as np # For numerical computations and handling arrays
import scipy.stats as stats # For statistical functions and probability distributions
import pandas as pd # For working with dataframes
# Define an example dataset
# Create a 1D NumPy array with some sample values (our dataset)
y = np.array([145, 125, 190, 135, 220, 130, 210, 3, 165, 165, 150, 350, 170, 180, 195, 440, 215, 135, 410, 40, 140, 175])
# Create an array with evenly spaced numbers within a given interval (0, 1, 2, ...) to use as the x-axis
# Use np.arange(start (optional, default = 0), stop = len(y), step (optional, default = 1))
x = np.arange(len(y))
# Visualize the dataset
# Create a scatter plot of the data using x = indices (0, 1, 2, ...) and y = dataset values
plt.scatter(x,y)
# Add labels to the x-axis and y-axis
plt.xlabel("Index (x)") # Describes what x-values represent
plt.ylabel("Data values (y)") # Describes what y-values represent
# Add a title to the plot
plt.title("Scatter Plot of Example Dataset")
# Display the plot
plt.show()
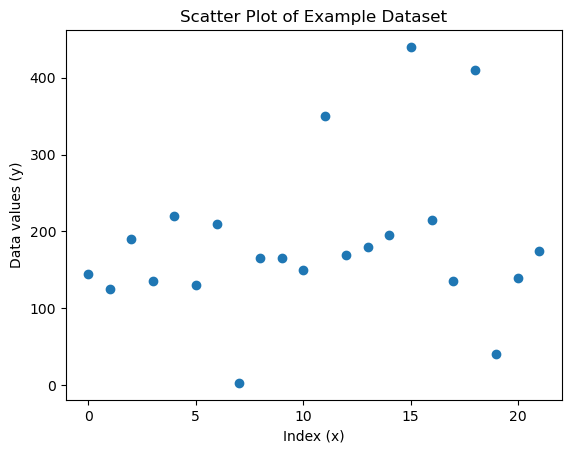
Most values are very close together (between 0.199 and 0.203). We have 3, 40, 350, 410, and 440 as potential outliers. Let’s apply a generalized ESD test.
Null hypothesis (\(H_{0}\)): there are no outliers in the data
Alternative hypothesis (\(H_{a}\)): there are up to 6 outliers in the data
# Define a function with loop to iterate over maximum number of outliers
def generalized_esd_test(data, max_outliers, alpha):
"""
Perform the Generalized ESD test for detecting multiple outliers in a dataset.
Parameters:
data (list or np.array): input numerical data
max_outliers (int): maximum number of outliers to test for
alpha (float): significance level (commonly 0.05 for 5%)
Returns:
dictionary (dict) containing
- outlier_indices: list of indices of detected outliers
- outliers: list of outlier values
- test_statistics: list of calculated test statistics R for each iteration
- critical_values: list of calculated critical values λ for each iteration
"""
# Convert data to numpy array for easier manipulation
data = np.array(data)
# Determine the length of the dataset
n = len(data)
# Lists to store data
outlier_indices = []
outliers = []
test_statistics = []
critical_values = []
# Copy of the data to modify iteratively
data_copy = data.copy()
# Loop and compute and compare test statistic R and critical value λ
for i in range(1, max_outliers + 1):
# Calculate test statistic R for this iteration
mean = np.mean(data_copy) # Mean of the dataset
std = np.std(data_copy, ddof=1) # Sample standard deviation
abs_diff = np.abs(data_copy - mean) # Absolute differences of each dataset value from the mean
max_abs_diff = np.max(abs_diff) # Largest absolute difference from the mean
R = max_abs_diff / std # Largest deviation divided by sample standard deviation, test statistic R
# Select the dataset value to remove
max_index = np.argmax(abs_diff) # Maximum absolute difference from the mean
actual_index = np.where(data == data_copy[max_index])[0][0] # Calculate the index of the maximum absolute difference in the original data
# Compute critical value λ for this iteration
p = 1 - alpha / (2 * (n - i + 1)) # Define p
t = stats.t.ppf(p, n - i - 1) # Critical value for two-tailed test
lambda_crit = ((n - i) * t) / (np.sqrt((n - i - 1 + t**2) * (n - i + 1))) # Formula for critical value λ
# Store values for inspection
outlier_indices.append(actual_index)
outliers.append(data_copy[max_index])
test_statistics.append(R)
critical_values.append(lambda_crit)
# Remove the detected outlier from the copy of data for the next iteration
data_copy = np.delete(data_copy, max_index)
# Build DataFrame for all iterations
df = pd.DataFrame({
"Iteration": range(1, len(test_statistics) + 1),
"Index": outlier_indices,
"Value": outliers,
"Test Statistic (R)": test_statistics,
"Critical Value (λ)": critical_values
})
# Add decision column: Was the suspected outlier flagged?
df["R > λ ?"] = df["Test Statistic (R)"] > df["Critical Value (λ)"]
return df
# Example usage of function
result = generalized_esd_test(y, 6, 0.05)
print(result)
Iteration Index Value Test Statistic (R) Critical Value (λ) R > λ ?
0 1 15 440 2.497556 2.757735 False
1 2 18 410 2.729992 2.733780 False
2 3 11 350 2.714963 2.708246 True
3 4 7 3 2.721414 2.680931 True
4 5 19 40 2.838520 2.651599 True
5 6 4 220 1.707766 2.619964 False
In this example, the largest number of outliers for which the test statistic is greater than the critical value (at the 5 % level) is five. We can conclude that there are five outliers in this dataset.
